已停用 啟用查詢紀錄

偶函數
ǒu hán shù
解釋
當函數y=f(x)的自變數x變號後,其值仍不改變時,即f(-x)=f(x),稱此類函數為「偶函數」。如y=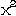 +2。
+2。
重編國語辭典
解釋
在數學裡,偶函數和奇函數是滿足著相對於加法逆元之特定對稱關係的函數. 這在數學分析的許多領域中都很重要,特別是在冪級數和傅立葉級數的理論裡. 其命名是因為冪函數的冪的奇偶性滿足下列條件:若n為一偶數,則函數x^n是偶函數,若n為一奇數,則為奇函數. 設f(x)為一實變數實值函數,則f為偶函數若下列的方程對所有在f的定義域內的x都成立: 幾何上,一個偶函數會關於y軸對稱,亦即其圖像在對y軸為軸對稱後不會改變. 偶函數的例子有|x|、x2、x4、cos(x)和cosh(x). 偶函數不可能是個雙射映射. 再次地,設f(x)為一個實變數實值函數,則f為奇函數若下列的方程對所有在f的定義域內的x都成立: : 或 f(-x) 0). * 通常,一個偶函數和一個奇函數的相加不會是奇函數也不會是偶函數;如x+x^2. * 兩個偶函數的相加為偶函數,且一個偶函數的任意常數倍亦為偶函數. (偶+偶 偶) * 兩個奇函數的相加為奇函數,且一個奇函數的任意常數倍亦為奇函數. (奇+奇 奇) * 兩個偶函數的乘積為一個偶函數. (偶×偶 偶) * 一個偶函數和一個奇函數的乘積為一個奇函數...閱讀更多
中文維基百科