有理函數

ㄧㄡˇㄌㄧˇㄏㄢˊㄕㄨˋ

yǒu lǐ hán shù

解釋

以有理式表示的函數。如ｆ(x)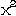＝＋3。

重編國語辭典

解釋

有理函數是可以表示為以下形式的函數： :，b_i不全為0. 有理數式是多項式除法的商，有時稱為代數分數. * 不失一般性可假設分子、分母互質. 若存在r0，使得(px+q)^r是分母Q(x)的因子，則有理函數存在垂直漸近線x 0. * 若m n+1，有斜漸近線. 只有一條水平漸近線有理函數的泰勒級數的係數滿足一個線性遞歸關係. 反之，若一個泰勒級數的係數滿足一個線性遞歸關係，它對應的函數是有理函數. 部分分式，又稱部分分數、分項分式，是將有理數式分拆成數個有理數式的技巧. 有理數式可分為真分式、假分式和帶分式，這和一般分數中的真分數、假分數和帶分數的概念相近. 真分式分子的次數少於分母的. 若有理數式的分母Q(x)可分解為數個多項式的積，其部分分數便是，其中h_n(x)是Q(x)的因子，A_n是次數不大於Q(x)/h_n(x)的多項式. # 分拆分子的次數是3，分母的是2，所以先將它轉成真分式和多項式的和（即帶分式）：因為，所以其中A和B是常數. 兩邊乘以，得即比較係數，得解得A 12. 故：也可以把x的特殊值代入等式來解出...閱讀更多

中文維基百科

MD5	SHA1
06c00312e7fcfed320640b6140963b14	4190b11c9177d08c15134ede78a695d55147fefc
什麼是雜湊

有理函數

ㄧㄡˇㄌㄧˇㄏㄢˊㄕㄨˋ

解釋

解釋

相關詞

你最近的查詢